
This page describes how various elemental value types are encoded. When decoding, you need to know what type to expect. In the next level, ColumnFormat, it is described how these expectations are encoded. Much later, after the MetaFormat is known then it is possible to interpret the values to a type.
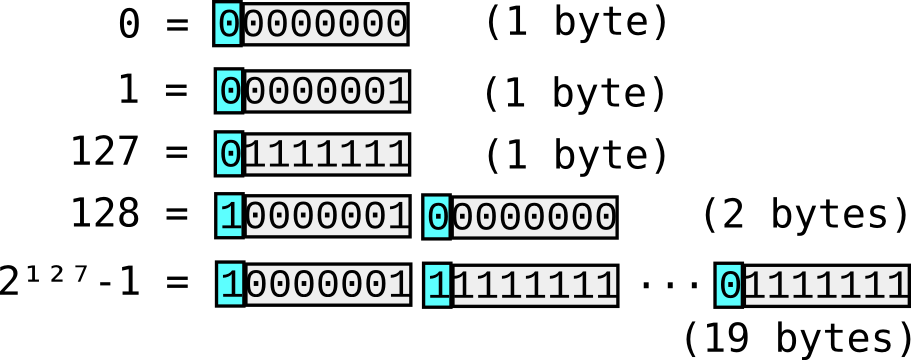
Figure 1. variable-length unsigned integer encoding; used by Perl and Google ProtocolBuffer.
Integers are widely encoded in binary by the design. For unsigned integers, a simple variable length integer encoding is used. This is essentially the same as that used by Perl's pack "w", $value and in Google's ProtocolBuffer.
This is a very straightforward convention. The top bit of every byte except the last is set, and the number is contained inside. The encoded number is reconstructed by assembling all of the 7-bit fragments together into a binary number.
There can be differences in whether the bytes appearing first or last are most significant ("Big Endian") or least significant ("Little Endian"). This standard is Big Endian, but that doesn't really make much difference to performance on Little Endian systems (which are most of the computers in the world) as they are not native machine words anyway.
In various places, it is possible to encode a number which may be negative. In JSON, the values are just stored in base 10. Signed integers appear in other parts of the Column Format as variable-length, twos-complement quantities.

Figure 2. The variable-length signed integer encoding used by this design. The sign bit is highlighted in green.
Perl's built-in function does not permit storing negative numbers, and in Google's ProtocolBuffers Encoding documentation, it is written (emphasis added):
The lower 7 bits of each byte are used to store the two's complement representation of the number in groups of 7 bits, ...
This standard actually implements that, and it is simple, straightforward and efficient. The diagram to the right shows how it works with various values.
However, ProtocolBuffers then does something very weird when it comes to signed integers:
If you use int32 or int64 as the type for a negative number, the resulting varint is always ten bytes long – it is, effectively, treated like a very large unsigned integer. If you use one of the signed types, the resulting varint uses ZigZag encoding, which is much more efficient.
I'm left thinking, so if I decode a 7-bit quantity with its high bit set, am I to interpret that as a negative number, as the "two's complement representation" written would imply, or as a 7-bit positive number?
I came to the conclusion that they'd simply stuffed up the spec. It wasn't a variable-length 2's complement number at all. The number is to be considered negative, if bit 63 in the number is set. The standard is effectively married to 64-bit integers, and I really didn't want that.
In fact they invented a whole new type code to work around this bug, even though the answer is obvious - simply extend the sign bit in the decoded number across the entire machine word. Conveniently, it's even a single instruction on x86 processors (SAR / SAL). When working with signed integers in C, the >> operator refers to this signed shift.
To "convert" a number N, decoded from X bytes, to a native signed integer of W bits width, you therefore use:
(int)( (unsigned int)N << (W-X*7) ) >> (W-X*7)
More likely, to "convert" a number Nt, decoded from X bytes, the lower 7 bits of each were packed into it from the top down, that's:
Nt << (W-X*7)
There are several second-order numeric types which are encoded. These are all built on the integer formats. Currently they all involve storing two variable length, signed integers.
| Name | Formula | Description | JSON |
|---|---|---|---|
| float | N × 2*M* | Floating point: general purpose, "real" numbers | (none) |
| decimal | N × 10*M* | Decimal precision values (eg money or IEEE decimal formats) | 100.1, 1.2345e+5 |
| rational | N ÷ M | Arbitrary precision rational numbers | 4/37, 12345/23941 |
Converting from the two integers N and M to a corresponding floating point value is trivial in each case; though see the below section for how "special" IEEE floating point values are encoded.
In JSON data form, there is no 'float', but instead 'decimal' is used. This is because in JSON you cannot have literals in hexadecimal, such as "0x1.ef0fp+0", as in C, Python, etc. It's possible to encode a true rational as a JavaScript expression, and you can express all floating point numbers precisely as a rational, but this is not recommended for general applications. Few if any JSON parsers will read it without exception anyway.
Architecture-dependent floats can be easily transformed into the underlying integers, through either directly accessing the bit fields of the floating point word (eg, from C), or using a relatively IEEE math (from other languages).
Only implementations and applications that care about precision of the values they are storing need implement output for decimal and rational; others need only know how to read them. It is also possible to specify in the MetaFormat that only particular encodings are allowed for a given type.
Again, it seems like the standard has ended up re-inventing the wheel by coming up with its own floating point representation. However, the need for this arose from actually trying to implement the output format.
Specifying a particular common format, such as IEEE 754-2008 binary64 (as ProtocolBuffers uses) was certainly the first choice. However, there are problems if the native float format is not binary64; this might seem unlikely, but it happens. And emitting 64-bit floats if that is not what your hardware is using can be problematic, too. Finally, if you are working with for instance 80-bit floats and the storage system loses 11 bits of precision when you put values in and out, this can be an annoyance.
The IEEE 754 standard is a good choice for a machine word, and makes computations fast and squeezes every bit of precision it can out of the available space. However the requirements of this standard are slightly different. It doesn't matter a lot if the stored size is slightly larger than the machine format, just so long as all platforms can read and write them.

Figure 3. How various single-precision floating-point values are converted to two integers for encoding
To understand the solution used in git db, it helps to understand how floating point formats work. The Wikipedia IEEE Float Page is at the time of writing quite useful and informative.
The idea with floating point is to reduce the problem of working with fractional values, to working with integers. Much as how when dealing with long multiplication on paper, you ignore the decimal points and then at the end put the point at the correct point. Floating poiNt arithmetic is just like this, but in binary instead of base 10.
So, the floating point number is essentially two (binary) numbers: a mantissa and an exponent. When you do something like a multiply, you multiply the two mantissas, leaving a much larger mantissa, add the exponents together and then "normalize" the result so that the mantissa is in range of the amount of space you have for it.
The essence of the floating point encoding is to take these two numbers from the float, adjust them so that they are in terms of N × 2*M*, and then store those. In terms of converting from IEEE 754 formats, this means subtracting a bias for the exponent, and usually putting a 1 at the front of the mantissa. The reason for this is that the only value which does not start with a 1 is 0, which is considered a special case.
Once you have expressed the number as N × 2*M*, it can then be reduced - while N is even, you can halve it and subtract one from M. Because of this, some floats end up encoding to a sequence smaller than the native float, but this is unusual.
There are some special cases required for full representation of IEEE floats, and these are described below.
In C, the conversion in and out is a matter of including the relevant floating point header file, and extracting the bits. This can all be done using fast integer math, without divisions, and without losing any precision.
In languages where such low-level manipulation of machine words is not available, conversion in is two IEEE math operations, and conversion out is three or more, such as:
scale = int(log(num) / log(2));
mantissa = int(num * 2**(MANTISSA_BITS - scale));
exp = scale - MANTISSA_BITS;
while ( int( (mantissa+1)/2 ) == mantissa/2 ) {
mantissa = mantissa / 2;
exp++;
}
_return(mantissa, exp);
MANTISSA_BITS would be 53 for binary64 (double precision) systems, 23 for binary32 (single precision) and so on. You may lose a few bits of precision with this approach, and it is slow - but it can be done. There is an obvious optimization, too - the final loop can be done with higher powers of 2, to reduce the two integers with fewer loop iterations. 0, the infinities and nan's will also require special case branches.
However complicated emitting one of these pairs is from a high level language, ignoring the exception cases which result in mantissa == 0, reconstructing is very simple:
num = mantissa * (2 ** exp)
Note, the difficulties around this format is not really down to the storage format; N × 2*M* is very simple and it is the IEEE 754 format which is (justifiably) more complicated.
This simplicity/space trade-off is quantified in the below table:
| Name | Common Name | Native Size | Encoded Size |
|---|---|---|---|
| binary16 | half precision | 2 bytes | 2-3 bytes |
| binary32 | single precision | 4 bytes | 2-6 bytes |
| binary64 | double precision | 8 bytes | 2-11 bytes |
| 8087-80 | "extended precision" | 10 bytes | 2-12 bytes |
| binary128 | quadruple precision | 16 bytes | 2-19 bytes |
Of course, only numbers which are "round numbers" in binary, like 192, 0.125 and 16777216 will get the most compact end of the size range regardless of the native float format.
The decimal representation is there primarily because most databases support a fixed-precision type, eg NUMERIC(9,2), and it should be possible to support this precisely when this is requested in the schema.
There is another use for decimal representation. For example, the number 0.2 (base 10) will be a recurring number expressed in binary (0.001100110011...) and cannot be converted exactly to an integer times a power of two.
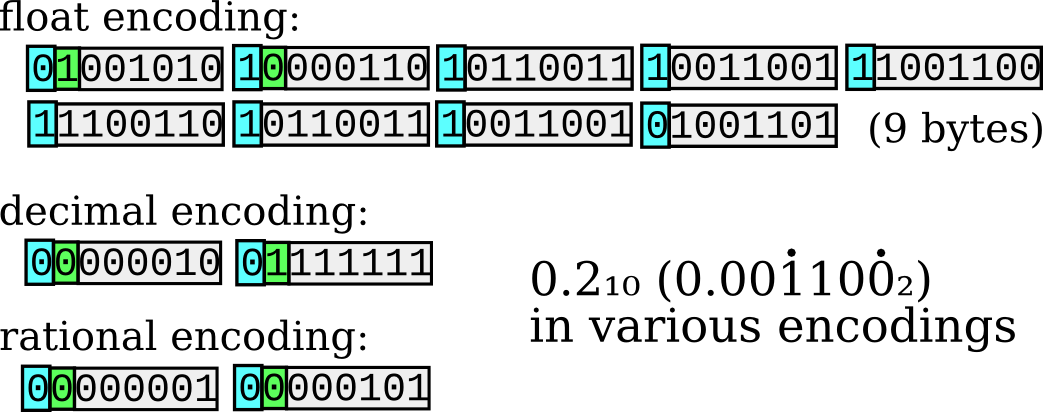
Figure 4. How the various encodings store "0.2"; the 'float' encoding assumes a binary64 source platform. You can see the reciprocal repeating itself through the digits, and the effect of ieee 754 rounding rules on the final bit.
205 × 2-10, the closest representation available in binary16, is 0.200 - not bad for 16 bits. In float format, at the same precision, you're looking at 3 bytes of storage space. Unpacked on a double precision platform, it will render as 0.2001953125.
3355443 × 2-24, for single precision, encodes to 5 bytes. In double precision, which most machines will use (and gcc can emulate on platforms which don't support it natively), you end up with 3602879701896397 × 2-54, taking a whopping 9 bytes to encode.
For the die-hard 8087 80-bit format, 3689348814741910323 × 2-64, encoding in 10 bytes, is actually the same size as the original float. If you happened to find yourself on some machine with the ieee128 format, 1038459371706965525706099265844019 × 2-112 encodes to an 18 byte sequence.
This highlights a point; much extra space is used for precision which isn't really there, and in fact it is never precisely the same as the simple string "0.2". Therefore, some implementations might choose to try converting floating point values to decimal before they are stored, and if the mantissa in decimal (rendered to the IEEE decimal rules) is significantly smaller than the maximum float mantissa value, then to store the value using the decimal encoding instead.
If an implementation does decide that "0.2" is a decimal, and not a floating point value, it can store it as 2 × 10-1, which is only 2 bytes and fully precise on all floating point platforms.
This format can store the set of rational numbers, and is included as alongside the other two-integer formats it is trivial to decode and infinitely expands the precisely representable numeric values. While N × 2M is an infinite set, there is another infinite set of other precise numeric values as well. Sure, there are useful irrationals one could precisely encode like (₁₂√2)⁵ - a major 3rd - but 4/3 is usually close enough to a third to tune a guitar.
In this format the numerator is a signed variable length integer, and the denominator is an unsigned one. The denominator may not be zero.

Figure 5. how the NFD representation of the string "Māori" is encoded. UTF-8 multi-byte sequences are similar to the varuint encoding, but use the top bit to indicate that the byte is a part of a multi-byte sequence.
These are encoded with a variable length unsigned integer, followed by a quantity of bytes. Neither the encoding nor the column format has any knowledge of UTF-8; however there are two standard types which have different functions depending on whether the content is a byte string, or text.